경사하강법(Gradient Descent) 쉽게 이해하기

기계학습을 배우면서 경사하강법, 경사감소법 등등 많은 단어를 접했지만,

대략적으로만 알고 실제로 무엇을 의미하는지 몰랐던 것 같다....

좀더 쉽고 간단하게 이해한것을 까먹지 않기 위해 적어둔다.

 

 

일단 경사하강법은 많은 기계학습 및 딥러닝(기계학습에 포함되지만 따로 분류하고?) 알고리즘들을 학습 시킬 때 사용되는 방법이다

 

가장 간단한 예제인 선형 회귀를 예로 들어보면,

선형회귀는 선형적으로 분포된 데이터를 가장 잘 표현하는 직선(일차 함수)를 찾는 것이다.

이때 직선을 y = wx + b로 표현한다면, 최적의 w와 b를 찾는 과정이 선형회귀 학습 과정이다.

이 최적의 w와 b를 찾기위해 경사하강법을 사용한다.

 

아래 그래프가 기온(x축)에 따른 군고구마 판매량(y축)이라고 할 때, 기온이 높아질수록 판매량은 감소할 것 이다.

사람은 딱 그래프를 보는 순간 아래와 같은 직선을 유추할 수 있다. 

 

그러나 컴퓨터는 사람과 달리 선을 바로 찾을 수 없다. (찍어서 맞을수도 있지만...)

그러므로 기계학습 모델에 경사하강법을 적용해서 직선을 찾도록 하였다.

 

임의의 w와 b로 직선을 생성하면, 직선과 각 데이터의 사이의 평균제곱오차(MSE, Mean Squared Error)를 구한다.

이때 n은 데이터(점)의 갯수이며, yi는 직선의 값(예측값), y^i는 실제값이므로 두 점의 거리를 나타낸다.

즉, 실제 값과 예측 값의 거리가 멀면 제곱에 의해서 값이 더 커진다.

이 MSE를 비용함수(Cost Function)이라고 부르고, 비용함수가 최소가 되도록 하는 w와 b를 찾으면 된다.

 

최적의 w와 b에서는 비용함수, 여기서는 MSE가 가장 작을테니 아래와 같은 2차 함수 형태가 나온다.

 

즉 컴퓨터는 아래 그림과 같은 값을 찾아야 하는데

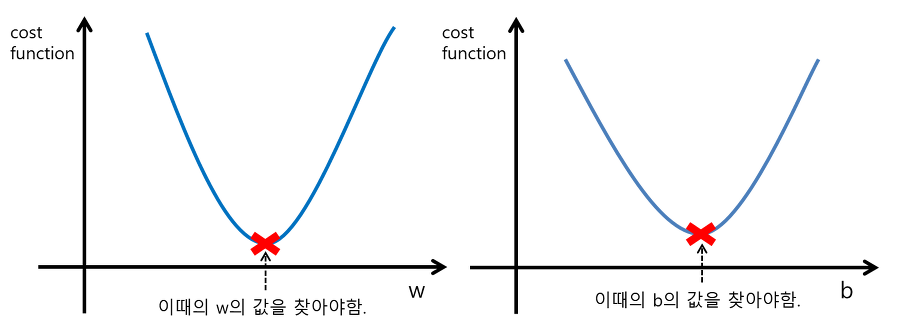
만약 비용 함수를 최소화하는 w를 찾으려면, 

임의의 w값을 설정한 뒤, w에서 비용함수를 w에 대해서 편미분해서 접선의 기울기를 구하고

이 접선의 기울기에 하이퍼파라미터로 설정한 학습률(Learning Rate) a를 곱해서 빼준다.

학습률이 너무 크면 최적의 w값을 지나서 넘어갈수도 있고, 너무 작으면 단계가 많아져 오래 걸릴 수 있다.

(적당한 학습률을 설정해야 한다.)

 

아래 그림에서는 초기 w의 위치에서 접선의 기울기가 음수이므로,  w - (-w'*a)를 하게되면 w+w'*a가 되므로 오른쪽으로 이동한다. 

이 과정을 반복하면 아래 그림과 같이 최적의 값을 찾을 수 있다.

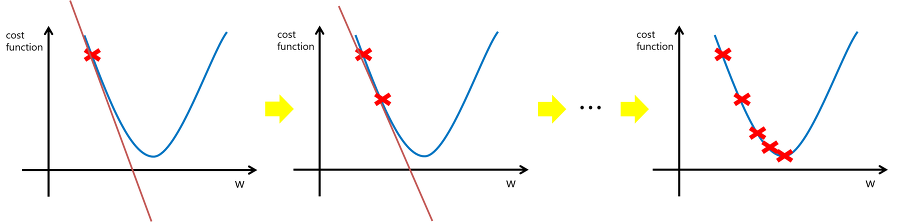
이런식으로 단계를 진행하면 기울기가(음수, 양수를 떠나서 절대값) 작아지므로 -> 경사가 감소한다고 표현한다.

그래서 경사 하강법이라 불린다.

 

실제로 w' (접선의 기울기)를 구할 때는 w한점에서는 그 '순간'의 변화량을 구할 수 없다.

그러므로 수치미분을 통해 구하게 된다. 수치미분은 임의의 두 점에서 함수 값들의 차이를 차분이라 하는데, 아주아주 작은 차분으로 미분하는 것을 수치 미분이라 한다.

즉, 위의 식에서 h가 0에 가깝게 줄어들면 x에서의 기울기로 놓는 것이다.

실제 컴퓨터에서는 h를 엄청 작게 (0^-10000으로) 놓게되면 반올림 오차가 발생한다고 한다.

그러므로 적당한 작은 값을 통해 구한다.

 

차분에는 전방 차분 (x와 x+h를 통해 구하는 방법)과 중앙 차분(x-h와 x+h를 통해 구하는 방법)이 있는데 뭐가 더 좋은지는 모르겠다...