정규 분포

위키에서 정규 분포의 정의를 보면

 

확률론과 통계학에서, 정규 분포(正規 分布, 영어: normal distribution) 또는 가우스 분포(Gauß 分布, 영어: Gaussian distribution)는 연속 확률 분포의 하나이다. 정규분포는 수집된 자료의 분포를 근사하는 데에 자주 사용되며, 이것은 중심극한정리에 의하여 독립적인 확률변수들의 평균은 정규분포에 가까워지는 성질이 있기 때문이다.

 

https://ko.wikipedia.org/wiki/%EC%A0%95%EA%B7%9C_%EB%B6%84%ED%8F%AC

정규 분포 - 위키백과, 우리 모두의 백과사전

 

라는 설명이 나온다. 즉, 정규 분포 == 가우스 분포이며, 가우스 분포는 가우스 정규 분포(Gaussian Normal Distribution)이다.

 

 

정규 분포는 연속 확률 분포(연속된 변수의 확률 분포를 표현)의 일종이다.

 ex) 사람들의 키를 160~190으로 가정했을 때, 160~170에서는 많고, 190으로 갈수록 해당 사람의 수가 줄어든다. 이것을 그림으로 표현하는게 연속 확률 분포이다. 이때 연속 확률 분포를 표현하는 그래프(종?에 가까운 모양, 그러나 다양한 모양이 나올 수 있음)를 확률 밀도 함수라고 한다.

 

이때 확률 밀도 함수의 모양이 이쁘게 종 모양으로 이루어진 경우를 정규 분포라 부른다.

정규 분포의 모양 예시

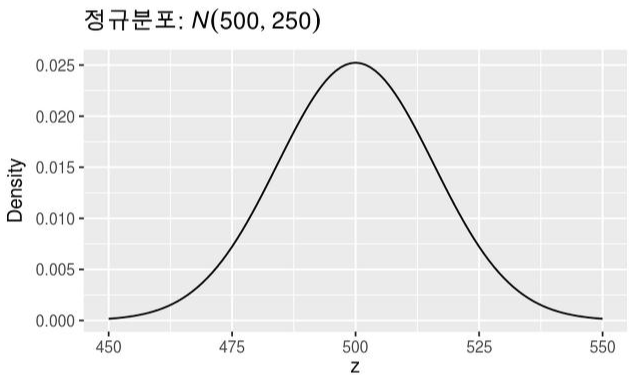
다시말해, 정규 분포란 다양한 연속 확률 분포를 표현하는 확률 밀도 함수가 존재하는데, 그 중 종 모양으로 표현되는 확률 밀도 함수이다.

또한 정규 분포의 가장 높은 지점은 평균을 의미한다.

 

실제로 다양한 데이터들이 정규 분포를 따르기 때문에, 다양한 데이터에서 분포를 모를 때 정규 분포로 가정한다.

(키, 몸무게, 시험 점수 등 다양한 측정값이 정규 분포를 따른다)

 

 

정규 분포를 이해하기 가장 좋은 예시는 동전 던지기이다.

사람이 동전(앞, 뒤만 존재)을 던졌을 때 앞면이 나오는 경우는 초반(실험 횟수가 적을 경우)에는 정규 분포와 다른 경우가 나올 수 있다.

예를들면 동전을 3번 던졌을 때 모두 앞면이 나올 수 있다. 이 경우에는 정규분포와 거리가 먼 그래프가 나온다. 그러나 횟수가 늘어나면 앞면과 뒷면이 나오는 경우의 수가 비슷해지고, 무한히 많은 경우를 비교한다면 50에 수렴하게된다.

횟수와 확률을 그래프로 표현하면 아래 그림과 같이 나온다. 동전을 100번 던졌을 경우에도 어느정도 정규 분포와 비슷한 모양이 나오지만, 횟수가 500번, 1000번으로 증가할수록 정규 분포와 더욱 유사해진다.

 

 

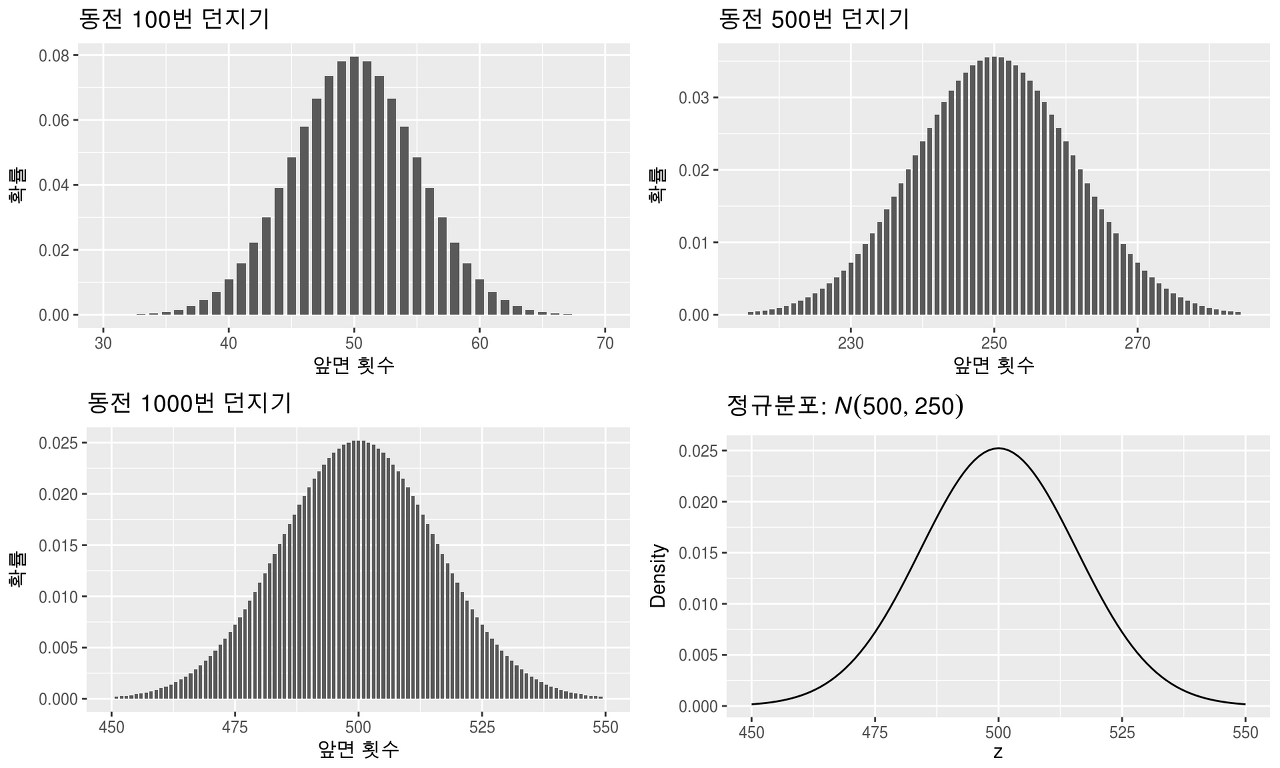
동전의 경우는 앞, 뒤가 나올 두가지 경우밖에 없으므로, 50%의 확률을 나타내는 가장 높은 지점을 기준으로 좌 우가 거의 동일하게 나온다. 그러면 확률이 다양한 경우라면, 그래프의 모양이 달라질까?라는 생각을 하게된다.

 

만약 주사위를 던지는 경우 1~6의 숫자를 얻을 수 있다.

이 중 주사위를 던져서 1이 나오는 경우를 실험한다면

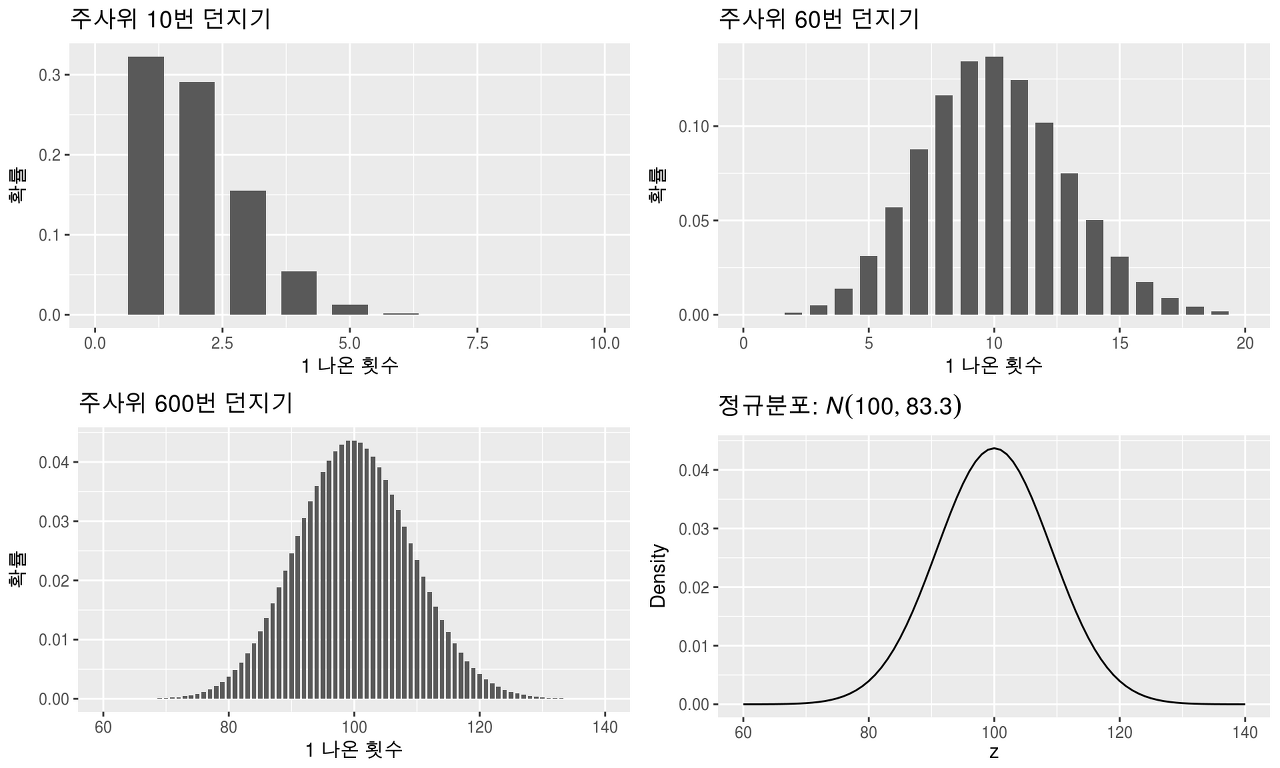
횟수가 늘어날수록 정규분포와 유사해지며, 좌우 대칭이 나온다.

 

 

정규 분포를 표현할 때는 평균 μ, 분산이 σ2인 정규분포를 N(μ,σ2)으로 표현한다.

위의 그래프에서 N(100, 83.3)은 평균이 100이며, 분산이 83.3인 정규 분포이다.