백준 / 2150 / Strongly Connected Component / 파이썬, python, pypy

2150번: Strongly Connected Component

Strongly Connected Component(SCC)에 대한 개념이 부족하여 찾아보았는데, 

SCC는 결국 시작지점으로 돌아올 수 있는 노드집합 == 사이클 여부로 이해하였다.

 

SCC 알고리즘은 크게 Kosaraju 알고리즘과 Tarjan 알고리즘이 있다고 한다.

두개의 알고리즘을 이해하려 하였을 때, Kosaraju 알고리즘이 더 이해하기 쉽고, 구현도 쉬울 것 같아서 사용하였다.

 

Kosaraju 알고리즘 동작 방식

kosaraju 알고리즘을 사용하려면 순방향 그래프와 역방향 그래프가필요하다.

 

1. 정방향 그래프를 사용하여 모든 노드에서 dfs를 실행한다.

    - 이때 dfs가 끝나는 순서대로 stack에 넣는다.

2. stack에서 pop을 하면서 역방향 그래프를 사용하여 dfs를 실행한다.

    - pop된 노드가 이미 방문된 노드라면 실행할 필요 X

    - 이때는 순서 상관없이 dfs를 통해 사용되는 모든 노드를 같은 SCC로 저장한다.

3. stack에 있는 모든 노드를 체크하면 모든 SCC를 구할 수 있다.

 

찾아보던 중 그림으로 잘 표현된 블로그가 있어 참고하였다.

(https://ca.ramel.be/166?category=935131)

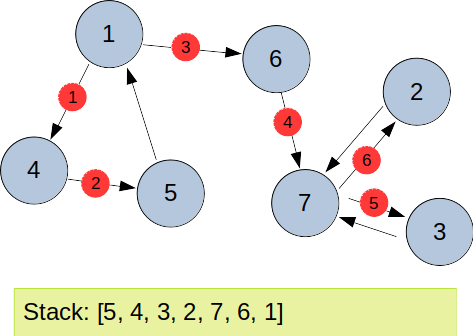
1번 노드에서 부터 시작하여 dfs 알고리즘으로 탐색해나간다면 가장 먼저 5에서 진행할 수 있는 노드가 없어 dfs 가 종료되게 된다. 따라서 5와 4의 순서대로 스택에 쌓이게 된다.

마찬가지로 dfs 탐색을 계속해나아간다면 아래와 같은 stack을 구할 수 있다.

이후 역방향 그래프를 이용하여 stack 에서 pop 되는 요소 순서대로 역방향 dfs 를 진행하게 된다. 아래 그림과 같이 stack 에서 가장 먼저 1번 노드가 pop 되게 된다.

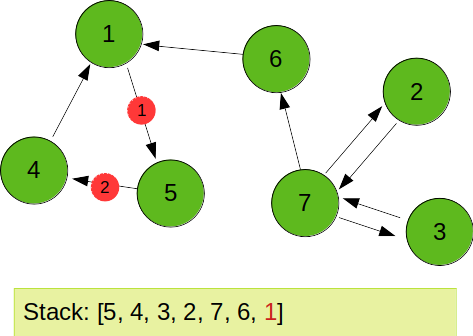
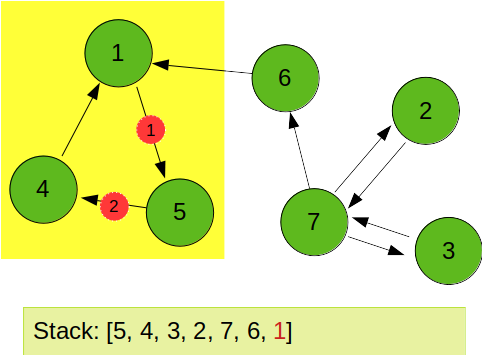
1번 노드에서 역방향 dfs 를 진행하면 5를 통해 4로 진행하여 1, 5, 4 가 한개의 SCC 로 묶임을 알 수 있다.

다음으로 pop 되는 6번 노드에서는 진행할 수 있는 노드가 없으므로 한개의 노드가 SCC 를 이루게 된다.

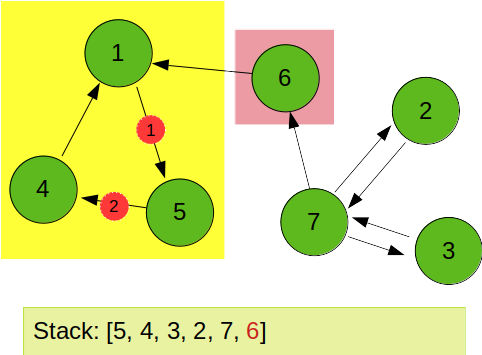
마지막으로 7에서 시작하는 역방향 dfs를 통해 7, 2, 3이 한개의 SCC로 묶이게 된다.

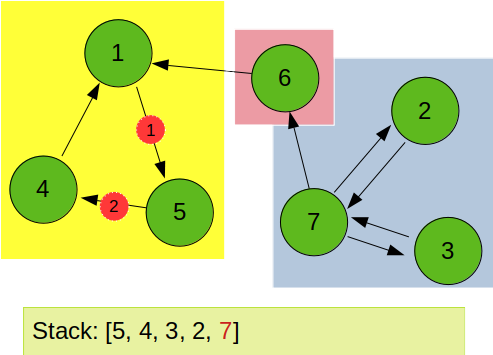
위 그림과 같은 방식으로 동작하며, 백준에서 원하는 출력은 각 SCC가 오름차순, 그리고 SCC 그룹의 시작도 오름차순으로 정렬하면 된다.

 

import sys
from collections import defaultdict, deque
sys.setrecursionlimit(10**6)
 
def dfs(cur):
    visited.add(cur)
 
    for next in forwardGraph[cur]:
        if next not in visited:
            dfs(next)
    stack.append(cur)
 
def reverseDfs(cur, scc):
    visited.add(cur)
    scc.append(cur)
 
    for next in reverseGraph[cur]:
        if next not in visited:
            scc = reverseDfs(next, scc)
    return scc
 
def kosaraju():
    global visited
    answer = []
    # 정방향 그래프를 돌면서 dfs 실행
    for i in range(1, V+1):
        if i not in visited:
            dfs(i)
 
    visited = set()
    while stack:
        scc = []
        cur = stack.pop()
 
        if cur in visited:
            continue
 
        answer.append(sorted(reverseDfs(cur, scc)))
    return answer
 
V, E = map(int, sys.stdin.readline().split())
forwardGraph = defaultdict(list)
reverseGraph = defaultdict(list)
 
for _ in range(E):
    A, B = map(int, sys.stdin.readline().split())
    forwardGraph[A].append(B)
    reverseGraph[B].append(A)
 
stack = []
visited = set()
answer = kosaraju()
 
print(len(answer))
for line in sorted(answer):
    print(*line, sep = ' ', end = ' -1\n')